地球流体中的多尺度相互作用
一个标量场T（如密度或速度分量）置身流场v中，如果两者都同时变化，则有可能发生由一个尺度子空间到另一个子空间的能量传输，从而导致相关结构（如漩涡）的产生。在MWT的框架下，这个传输（记作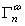
）可以严格地得到（Liang & Robinson, 2005; 2007）：
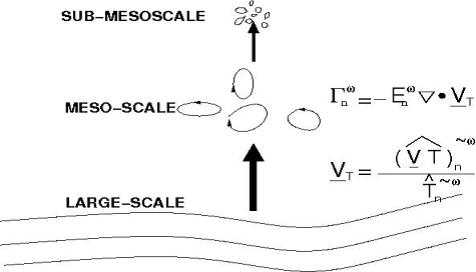
其中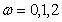
代表大、中、小尺度（或次中尺度）子空间， 
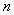代表时间步 ， 是
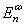子空间的能量，而
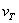被称为T-耦合速度， 
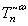（加上一帽子）为标量场T在子空间
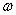、时间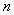上的多尺度子空间变换。 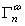有一个很好的性质，即
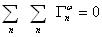
意即这种传输只是一种子空间之间的能量再分配，它不会产生也不会耗去能量，这一点与以往基于经验的公式非常不一样。为区别起见我们称之为“正则传输”(canonical transfer)。
在公式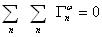中，将T换成流速的分量则可得到正则动能传输；换成扰动密度则得到正则有效未能传输。此二者被证明精确地对应着经典地球流体力学中的正压失稳与斜压失稳，而又没有经典理论中全局性的局限，能真实地表征流体失稳过程的时间间隙性与空间局地性。
考虑一个郭晓岚正压急流模型（Kuo’s Model），急流失稳必须满足一些必要条件(如Rayleigh条件、Kuo条件)。考虑一个特殊流速剖面（见下图），整体上满足这些条件满足，但在图b中的两个拐点处Kuo条件局地不成立，所以在这两点附件流体一定是稳定的。
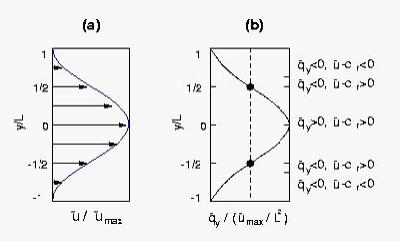
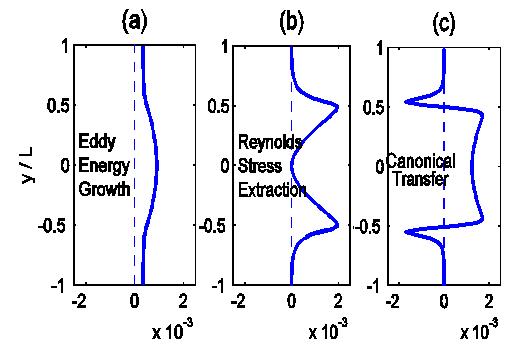
然而，所求得的扰动能量增长（下图a）在所有区域都是正值，可见在这里用扰动增长并不能诊断出两个拐点的不稳定性—观测到的“不稳定”并不一定就是真的不稳定；用传统的雷诺应力的概念得出的能量传输如图b示，它告诉我们两个转戾点处最不稳定，显然这是错误的；而我们的正则传输（图c）精确地反映了这个稳定性结构：虽然整体上急流不稳定，在两个拐点附近是稳定的，而且这里能量是由扰动向平均流作反向传输。
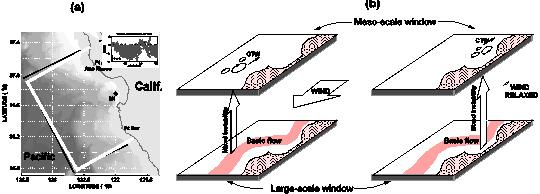
用以上这套理论我们做了几个应用。我们发现，一些外在看来非常复杂的海洋问题其内部过程常常有章可循。一个例子是对美国西岸Monterey湾动力过程的研究(Liang & Robinson, 2009)。Monterey湾（见下图a）乃美国一重要海域，但流况非常复杂。美国海洋学家常年在此进行调查研究，迄今为止已有七十多年了，但其动力机制一直不清楚，直到最近才由Liang & Robinson（2009）用上述理论取得突破。我们发现，此处复杂的动力过程主要为湾内以及湾南两处的稳定性所控制。如上图b所示，当有利于上升流的南向风一吹，湾南外海混合失稳，形成的中尺度漩涡以沿岸波的方式向北传播；当南向风停止后，湾南变得稳定，但湾内发生混合失稳，形成的涡旋同样向北传播，其模态振幅集中在温跃层附近。用我们的理论还发现Monterey湾的上升流的产生与经典的机制不相干，而是由非线性混合失稳所致；风对海洋的驱动也与传统的观点完全不一致，它是通过储存能量于大尺度子空间然后由洋流失稳 传递到中尺度子空间来完成这驱动过程的。这项被审稿人称为“加州海流系统研究中的主要进展”的工作是我们前述理论的一个直接应用的结果。
相关文章下载：
Zhao, Y. B., X. San Liang, 2018: On the inverse relationship between the boreal wintertime Pacific jet strength and storm-track intensity. J. Clim., 31